YK菌

一、概述——为什么要学数据结构

# 一、概述——为什么要学数据结构

你一定听说过这句话： 程序 = 数据结构 + 算法。 今天我们来研究的数据结构

现在的计算机主要是处理一些非数值计算，也就是处理一些字符、表格、图像等一些具有结构的数据。

数据结构是一门研究非数值计算程序设计中操作对象，以及这些对象之间的关系和操作的学科。

上面这句严版较菜里的定义比较拗口，其实简单来说数据结构就是研究如何合理地组织数据、高效地处理数据问题的。

可以组织、处理数据了，再加上一些算法，就可以组成程序，用来解决一些实际的问题。

今天我们主要来介绍数据结构的一些基本概念

# 二、数据有哪些结构

数据结构（Data Structure）是相互之间存在一种或多种特定关系的数据元素的集合。

数据结构主要分为逻辑结构和存储结构两个层级。逻辑结构顾名思义就是逻辑上的结果，是人类自己总结出来并给他命名的结构，而存储结构就是真正将这些数据存储在计算机中所使用的结构。

# 1. 逻辑结构

# （1）集合结构

集合的概念我们在高中就已经学过，这里也类似。集合结构的意思就是将这些数据放在同一个集合中，它们之间没有什么关系。

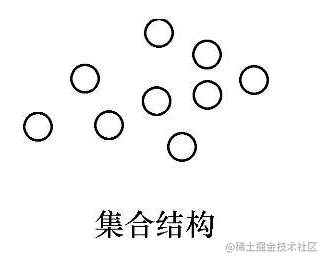
image.png

举一个例子：在一个新入学的班级里，学生看作数据，那班级就可以看作是一个集合结构

# （2）线性结构

线性结构中的数据具有一对一的关系

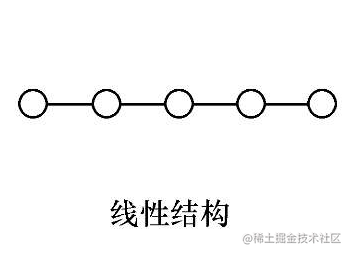
image.png

比如说，这个班级要将学生进行排列，比如是按照入学报道顺序进行排列，这就将组成一个线性结构。

线性结构包括我们熟悉的线性表、栈、队列、字符串、数组等

# （3）树结构

树结构中的数据具有一对多的关系

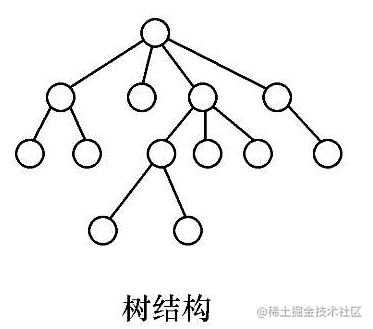
image.png

比如这个班级中要选出班长、小组长，这里班长管理着小组长，小组长管理着组员，这就形成了一个树结构。

# （4）图结构或网状结构

图结构中的数据具有多对多的关系

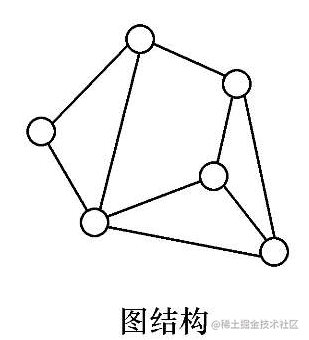
image.png

比如说这个班级，大家熟悉了之后，每位同学都有了很多朋友，朋友也有很多朋友，这就形成了一个图结构

# （5）小结

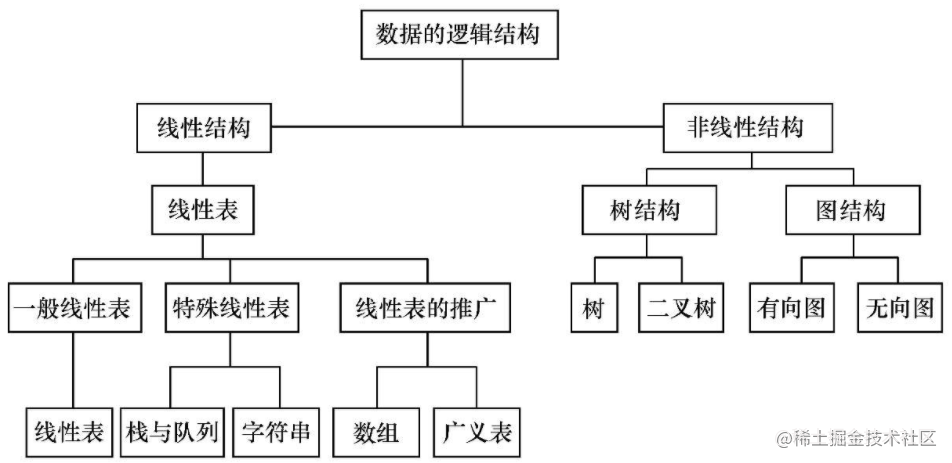
image.png

# 2. 存储结构

将数据存储在计算机中，需要存储结构，也称为物理结构。可以分为顺序存储结构和链式存储结构两种。

# （1）顺序存储结构

顺序存储结构是借助数据元素在存储器中的相对位置来表示数据之间的逻辑关系，顺序存储结构要求所有的元素依次存放在一片连续的存储空间中。

image.png

# （2）链式存储结构

链式存储结构是借助指针表示数据元素之间的逻辑关系，链式存储结构无需占用一整块存储空间。但为了表示结点之间的关系，需要给每个结点附加指针字段，用于存放后继元素的存储地址。

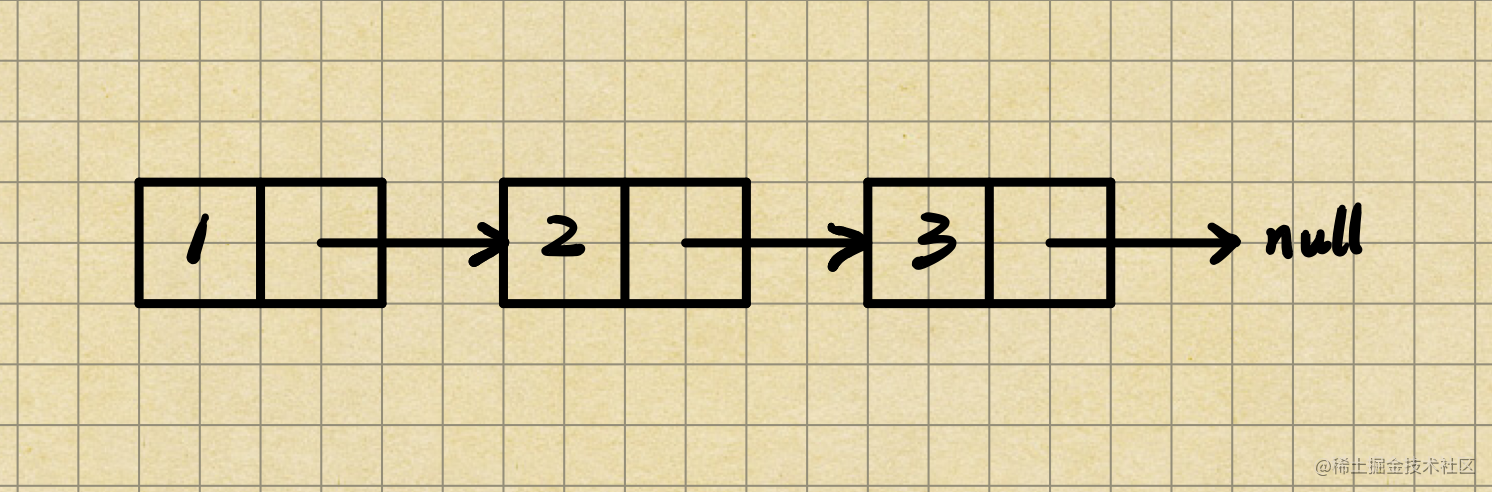
image.png

由于JavaScript中没有指针，但是JavaScript有引用类型。引用也是指向地址的，所以可以使用引用类型来建立结点之间的链接关系。 这里可以看我之前的博文：设计单链表 (opens new window) 和 设计双链表 (opens new window)

# 三、总结

  1. 数据结构是一门研究非数值计算程序设计中操作对象，以及这些对象之间的关系和操作的学科

  2. 数据结构包括两个方面的内容：数据的逻辑结构和存储结构。同一逻辑结构采用不同的存储方法，可以得到不同的存储结构

    1. 逻辑结构是从具体问题抽象出来的数学模型，从逻辑关系上描述数据，它与数据的存储无关。根据数据元素之间关系的不同特性，通常有四类基本逻辑结构：集合结构、线性结构、树形结构和图状结构

    2. 存储结构是逻辑结构在计算机中的存储表示，有两类存储结构：顺序存储结构和链式存储结构

# 四、练习

（1）在数据结构中，从逻辑上可以把数据结构分成（ ）。

  • A. 动态结构和静态结构
  • B. 紧凑结构和非紧凑结构
  • C. 线性结构和非线性结构
  • D. 内部结构和外部结构

（2）与数据元素本身的形式、内容、相对位置、个数无关的是数据的（ ）。

  • A. 存储结构
  • B. 存储实现
  • C. 逻辑结构
  • D. 运算实现

（3）通常要求同一逻辑结构中的所有数据元素具有相同的特性，这意味着（）。

  • A. 数据具有同一特点
  • B. 不仅数据元素所包含的数据项的个数要相同，而且对应数据项的类型要一致
  • C. 每个数据元素都一样
  • D. 数据元素所包含的数据项的个数要相等

（4）下述（）与数据的存储结构无关。

  • A. 栈
  • B. 双向链表
  • C. 散列表
  • D. 线索树
  • E. 循环队列

（5）连续存储设计时，存储单元的地址（）

  • A. 一定连续
  • B. 一定不连续
  • C. 不一定连续
  • D. 部分连续，部分不连续

（6）以下属于逻辑结构的是（）

  • A. 顺序表
  • B. 散列表
  • C. 有序表
  • D. 单链表

首先复习一下数据结构

  • 数组
  • 栈
  • 队列
  • 链表
  • 树（这里我们着重讲二叉树）

# 数组

一般来说，数组都对应着一段连续的内存，但是在JS中不一定。因为JS中的数组可以存放任意类型的数据。

如果存放的都是同一种类型的数据，那就是占用的连续内存；如果定义了不同类型的元素，那就不是连续的内存。JS底层使用哈希映射分配内存空间，是由对象链表来实现的。

# 创建数组

const arr1 = [1, 2, 3, 4]  
const arr2 = new Array()
const arr3 = []
const arr4 = new Array(7) // 创造指定长度的空数组
const arr5 = (new Array(7)).fill(1) // 创造指定长度的数组，初始值为1

# 遍历数组

  1. for循环
const len = arr.length // 将数组长度缓存，这样就不用每次循环都要查询
for(let i = 0; i < len; i++){
  console.log(arr[i], i)
}
  1. forEach
arr.forEach((item, index)=>{
  console.log(item, index)
})
  1. map
const newArr = arr.map((item, index)=>{
  console.log(item, index)
  return item + 1
})

# 二维数组

const arr = [
  [1,2,3,4,5],
  [1,2,3,4,5],
  [1,2,3,4,5],
  [1,2,3,4,5],
  [1,2,3,4,5]
]
console.log(arr[i][j]) // i表示行，j表示列

初始化的坑

const arr =(new Array(7)).fill([])

当给 fill 传递一个入参时，如果这个入参的类型是引用类型，那么 fill 在填充坑位时填充的其实就是入参的引用，也就是说层的数组都是同一个数组，操作一个会导致所有的都会改变

所以应该使用for循环来初始化一个二维数组

const len = arr.length
for(let i = 0; i < len; i++){
  arr[i] = []
}

遍历二维数组中的所有元素当然就要使用二重for循环

// 缓存外部数组的长度
const outerLen = arr.length
for(let i=0;i<outerLen;i++) {
    // 缓存内部数组的长度
    const innerLen = arr[i].length
    for(let j=0;j<innerLen;j++) {
        // 输出数组的值，输出数组的索引
        console.log(arr[i][j], i, j)
    }
}

# 数组上的一些常用的方法

Array - JavaScript | MDN (mozilla.org) (opens new window)

【JS】你不得不知道的JavaScript数组相关知识【全面总结】复习专用 - 掘金 (juejin.cn) (opens new window)

# 数组中添加元素的方式

  1. unshift 方法-添加元素到数组的头部

  2. push 方法-添加元素到数组的尾部

  3. splice 方法-添加元素到数组的任何位置

# 数组中删除元素的三种方法

  1. shift 方法-删除数组头部的元素

  2. pop 方法-删除数组尾部的元素

  3. splice 方法-删除数组任意位置的元素

# reduce

# 栈和队列

栈（Stack）——只用 pop 和 push 完成对增删的“数组”，是一种后进先出(LIFO，Last In First Out)的数据结构。

队列（Queue）——只用 push 和 shift 完成增删的“数组”，是一种先进先出（FIFO，First In First Out）的数据结构。

# 链表

数组和链表是同一级别的概念，是数据的存储结构的两种形成，顺序存储和链式存储。逻辑上都是顺序的数据结构。

707. 设计链表 - 力扣（LeetCode） (leetcode-cn.com) (opens new window)

链表是由一个个结点组合而成的，结点存储值与下一个结点的引用，在js中是用对象来存储的。

{
    // 数据域
    val: 1,
    // 指针域，指向下一个结点
    next: {
        val:2,
        next: ...
    }
}

既然是对象存储的，那就需要构造函数来创建结点了。

function ListNode(val) {
    this.val = val;
    this.next = null;
}

创建结点对象

const node = new ListNode(1)  
node.next = new ListNode(2)

# 链表元素添加

image.png

// 如果目标结点本来不存在，那么记得手动创建
const node3 = new ListNode(3)     
// 把node3的 next 指针指向 node2（即 node1.next）
node3.next = node1.next
// 把node1的 next 指针指向 node3
node1.next = node3

# 链表元素删除

在涉及链表删除操作的题目中，重点不是定位目标结点，而是定位目标结点的前驱结点。

# 链表元素访问

// 记录目标结点的位置
const index = 10  
// 设一个游标指向链表第一个结点，从第一个结点开始遍历
let node = head  
// 反复遍历到第10个结点为止
for(let i=0;i<index&&node;i++) {
    node = node.next
}

# 数组与链表

  • 链表的插入/删除效率较高，而访问效率较低；
  • 数组的访问效率较高，而插入效率较低。

# 树和二叉树

树的基本概念

  • 树的层次计算规则：根结点所在的那一层记为第一层，其子结点所在的就是第二层，以此类推。
  • 结点和树的“高度”计算规则：叶子结点高度记为1，每向上一层高度就加1，逐层向上累加至目标结点时，所得到的的值就是目标结点的高度。树中结点的最大高度，称为“树的高度”。
  • “度”的概念：一个结点开叉出去多少个子树，被记为结点的“度”。比如我们上图中，根结点的“度”就是3。
  • “叶子结点”：叶子结点就是度为0的结点。在上图中，最后一层的结点的度全部为0，所以这一层的结点都是叶子结点。

二叉树的概念

  • 它可以没有根结点，作为一棵空树存在
  • 如果它不是空树，那么必须由根结点、左子树和右子树组成，且左右子树都是二叉树。如下图：

二叉树不能被简单定义为每个结点的度都是2的树。普通的树并不会区分左子树和右子树，但在二叉树中，左右子树的位置是严格约定、不能交换的。

# 二叉树的存储

在 JS 中，二叉树使用对象来定义。它的结构分为三块：

  • 数据域
  • 左侧子结点（左子树根结点）的引用
  • 右侧子结点（右子树根结点）的引用
// 二叉树结点的构造函数
function TreeNode(val) {
    this.val = val;
    this.left = null;
    this.right = null;
}

image.png

# 二叉树的遍历

【LeetCode】二叉树的结构与遍历 - 掘金 (juejin.cn) (opens new window)

  • 【先序遍历】 根结点 -> 左子树 -> 右子树
  • 【中序遍历】 左子树 -> 根结点 -> 右子树
  • 【后序遍历】 左子树 -> 右子树 -> 根结点

# 先序遍历

144. 二叉树的前序遍历 - 力扣（LeetCode） (leetcode-cn.com) (opens new window)

【先序遍历】 根结点 -> 左子树 -> 右子树

function preorder(root){
  // 递归边界
  if(!root) return

  // 输出当前遍历的结点值
  console.log(root.val)
  // 递归遍历左子树 
  preorder(root.left)
  // 递归遍历右子树
  preorder(root.right)
}

# 中序遍历

94. 二叉树的中序遍历 - 力扣（LeetCode） (leetcode-cn.com) (opens new window)

【中序遍历】 左子树 -> 根结点 -> 右子树

function preorder(root){
  // 递归边界
  if(!root) return

  // 递归遍历左子树 
  preorder(root.left)
  // 输出当前遍历的结点值
  console.log(root.val)
  // 递归遍历右子树
  preorder(root.right)
}

# 后序遍历

145. 二叉树的后序遍历 - 力扣（LeetCode） (leetcode-cn.com) (opens new window)

【后序遍历】 左子树 -> 右子树 -> 根结点

function preorder(root){
  // 递归边界
  if(!root) return

  // 递归遍历左子树 
  preorder(root.left)
  // 递归遍历右子树
  preorder(root.right)
  // 输出当前遍历的结点值
  console.log(root.val)
}

# 时间复杂度

算法的时间复杂度，它反映的不是算法的逻辑代码到底被执行了多少次，而是随着输入规模的增大，算法对应的执行总次数的一个变化趋势。

补充知识 对数

logN 默认是以2为低的对数

log1024相当于问“将多少个2相乘的结果为1024” 即 2的多上次方是1024？ 答案是10

image.png

# 空间复杂度

空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度。和时间复杂度相似，它是内存增长的趋势。

# 数组的应用

# 两数之和

当发现自己的代码里有两层循环时，先反思一下，能不能用空间换时间，把它优化成一层循环。

几乎所有的求和问题，都可以转化为求差问题

利用Map

# 合并两个有序数组

双指针法

双指针法一方面可以做到空间换时间；另一方面，也可以降低问题的复杂度

双指针法用在涉及求和、比大小类的数组题目里时，大前提往往是：该数组必须有序。否则双指针根本无法帮助我们缩小定位的范围，压根没有意义。

# 三数之和

对撞指针 - 关键词：“有序”和“数组”

即使题目没有给有序，我们也可以自己手动排序

# 字符串的应用

# 反转字符串

// 定义被反转的字符串 
const str = 'juejin' 

// 定义反转后的字符串
const res = str.split('').reverse().join('')

console.log(res) // nijeuj

# 判断一个字符串是否是回文字符串

回文：要想到 对称性 和 双指针

# 字符串匹配

/**
 * 构造函数
 */
const WordDictionary = function () {
  // 初始化一个对象字面量，承担 Map 的角色
  this.words = {}
};

/**
  添加字符串的方法
 */
WordDictionary.prototype.addWord = function (word) {
  // 若该字符串对应长度的数组已经存在，则只做添加
  if (this.words[word.length]) {
    this.words[word.length].push(word)
  } else {
    // 若该字符串对应长度的数组还不存在，则先创建
    this.words[word.length] = [word]
  }

};

/**
  搜索方法
 */
WordDictionary.prototype.search = function (word) {
  // 若该字符串长度在 Map 中对应的数组根本不存在，则可判断该字符串不存在
  if (!this.words[word.length]) {
    return false
  }
  // 缓存目标字符串的长度
  const len = word.length
  // 如果字符串中不包含‘.’，那么一定是普通字符串
  if (!word.includes('.')) {
    // 定位到和目标字符串长度一致的字符串数组，在其中查找是否存在该字符串
    return this.words[len].includes(word)

  }

  // 否则是正则表达式，要先创建正则表达式对象
  const reg = new RegExp(word)

  // 只要数组中有一个匹配正则表达式的字符串，就返回true
  return this.words[len].some((item) => {
    return reg.test(item)
  })
};

# 字符串与数字之间的转换问题

正则表达式

/\s*([-\+]?[0-9]*).*/
  • \s 这个符号，意味着空字符，它可以用来匹配回车、空格、换行等空白区域，这里，它用来被匹配空格。
  • * 这个符号，跟在其它符号后面，意味着“前面这个符号可以出现0次或多次。
  • \s*，这里的意思就是空格出现0次或多次，都可被匹配到。
  • () 圈住的内容，就是我们要捕获起来额外存储的东西。
  • []中的匹配符之间是“或”的关系，也就是说只要能匹配上其中一个就行了。
  • [-\+]，-不必说匹配的是对应字符，这个\+之所以加了一个斜杠符，是因为+本身是一个有特殊作用的正则匹配符，这里我们要让它回归+字符的本义，所以要用一个\来完成转义。
  • [0-9]*结合咱们前面铺陈的知识，这个就不难理解了，它的意思是 0-9 之间的整数，能匹配到0个或多个就算匹配成功。
  • .这个是任意字符的意思，.*用于字符串尾部匹配非数字的任意字符。
  • 我们看到.*是被排除捕获组之外的，所以说这个东西其实也不会被额外存储，它被“摘除”了。

JS 的正则相关方法中， test()方法返回的是一个布尔值，单纯判断“是否匹配”。要想获取匹配的结果，我们需要调度match()方法。match() 方法是一个在字符串中执行查找匹配的String方法，它返回一个数组，在未匹配到时会返回 null。

// 入参是一个字符串
const myAtoi = function(str) {
    // 编写正则表达式
    const reg = /\s*([-\+]?[0-9]*).*/
    // 得到捕获组
    const groups = str.match(reg)
    // 计算最大值
    const max = Math.pow(2,31) - 1
    // 计算最小值
    const min = -max - 1
    // targetNum 用于存储转化出来的数字
    let targetNum = 0
    // 如果匹配成功
    if(groups) {
        // 尝试转化捕获到的结构
        targetNum = +groups[1]
        // 注意，即便成功，也可能出现非数字的情况，比如单一个'+'
        if(isNaN(targetNum)) {
            // 不能进行有效的转换时，请返回 0
            targetNum = 0
        }
    }
    // 卡口判断
    if(targetNum > max) {
        return max
    } else if( targetNum < min) {
        return min
    }
    // 返回转换结果
    return targetNum
};

# 链表

  • 链表的处理：合并、删除等（删除操作画个记号，重点中的重点！）
  • 链表的反转及其衍生题目
  • 链表成环问题及其衍生题目

# 合并两个有序链表

# 链表结点的删除

上次更新: 2022/4/18 18:10:13

排序算法