在这里插入图片描述 @[toc]

# 树类

这里讨论的基本上都是二叉树

# 树的结构

function TreeNode(val, left, right) {
	this.val = (val===undefined ? 0 : val)
	this.left = (left===undefined ? null : left)
	this.right = (right===undefined ? null : right)
}

# 树的遍历

在这里插入图片描述

# 深度优先遍历DFS （递归）

function DFS(root) {
	if (root === null) return;
	DFS(root.left);
	DFS(root.right);
}

# 深度优先遍历DFS （栈）

其实可以不用递归，小伙伴们可以在纸上画一画，等我有时间了再做几个图吧

function DFS(root) {
  const stack = [];
  stack.push(root);
  
  while (stack.length > 0) {
    root = stack.pop();
    if (root.right) stack.push(root.right);
    if (root.left) stack.push(root.left);
  }
}

# 广度优先遍历BFS （队列）

function BFS(root){
	const queue = [];
	queue.unshift(root);
	
	while(queue.length > 0) {
		root = queue.pop();
		if(root.left) queue.unshift(root.left);
		if(root.right) queue.unshift(root.right);
	}
}

# 94. 二叉树的中序遍历

中序遍历是先遍历左子树，然后访问根节点，然后遍历右子树。 ==左-中-右== https://leetcode-cn.com/problems/binary-tree-inorder-traversal/ (opens new window)

# 144. 二叉树的前序遍历

https://leetcode-cn.com/problems/binary-tree-preorder-traversal/ (opens new window)

# 145. 二叉树的后序遍历

https://leetcode-cn.com/problems/binary-tree-postorder-traversal/ (opens new window)

前序：根左右；中序：左根右；后序：左右根；中序常用来在二叉搜索数中得到递增的有序序列；后序可用于数学中的后缀表示法，结合栈处理表达式，每遇到一个操作符，就可以从栈中弹出栈顶的两个元素，计算并将结果返回到栈中；

# 【解法一】递归DFS

/**
 * @param {TreeNode} root
 * @return {number[]}
 */
function inorderTraversal(root) {
  // 定义一个结果数组，用来保存遍历的节点的值
  const result = [];

  // 定义递归函数
  function inorder(root) {
    // 递归出口，直到节点为空，退出递归
    if (root === null) return;
    
	// 【三种遍历方式更换顺序即可】
    // 递归调用，传入根节点的左孩子
    inorder(root.left);
    // 【中序遍历：左 - 中 - 右】
    // 将根节点的值放入result数组中
    result.push(root.val);
    // 递归调用，传入根节点的右孩子
    inorder(root.right);
  }

  // 执行递归函数 表示当前遍历到root节点的答案
  inorder(root);

  return result;
}

在这里插入图片描述

# 【解法二】非递归迭代法 - 栈

非递归，用一个栈

# 中序遍历

用一个栈和循环来模拟递归操作

遍历这颗树和栈，用while循环

function inorderTraversal(root) {
    const result = []
    const stack = []
    // 遍历树，结束终点：节点为空且栈为空
    while(root || stack.length > 0){
        // 遍历 root节点及其所有左孩子 入栈
        while(root){
            stack.push(root)
            root = root.left
        }
        // 左孩子遍历完入栈了，栈顶元素 出栈 【左-中】
        root = stack.pop()
        // 中序【左 - 中 - 右】 【左-中】
        result.push(root.val)
        // 指向右孩子，没有就是null，下次循环就会出栈一个元素
        root = root.right
    }

    return result
}

在这里插入图片描述

# 前序遍历

var preorderTraversal = function(root) {
    const result = []
    const stack = []
    while(root || stack.length > 0){
        while(root){
        	// 【前序：中 - 左 - 右】
            result.push(root.val)
            stack.push(root)
            root = root.left
        }
        root = stack.pop()
        root = root.right
    }
    return result
};

在这里插入图片描述

# 后序遍历（重难点）

var postorderTraversal = function(root) {
    const result = []
    const stack = []
    // 用来标记节点
    let prev = null
    while(root || stack.length > 0){
        while(root){
        	// 遍历节点左孩子到底【左】
            stack.push(root)
            root = root.left
        }
        // 栈顶出栈一个节点进行下面操作
        root = stack.pop()
        
        // 【后序：左 - 右 - 中】
        
        // 有右孩子，且右孩子没有被标记过，就将右孩子入栈，再while遍历右孩子
        if(root.right !== null && root.right !== prev){
			// 节点进栈，指针移向右孩子，再去循环 【右】
			stack.push(root)
			root = root.right
		}else {
			// 此时，没有右孩子【左-右-中】，或者有右孩子，但是被标记过了的【中】
			// 将节点的值存入结果数组
			result.push(root.val)
			// 存过的节点进行标记
			prev = root
			// 节点清空
			root = null
		}
    }
    return result
};

在这里插入图片描述

# 【解法三】Morris 中序遍历

将二叉树转化为链表，即每一个node都只可能有右孩子

function inorderTraversal(root) {
  const result = [];
  let predecessor = null;
  
  while (root !== null) {
  
    if (root.left) {
      // predecessor 节点就是当前 root 节点向左走一步，然后一直向右走至无法走为止
      predecessor = root.left;
      
      while (predecessor.right && predecessor.right !== root) {
        predecessor = predecessor.right;
      }
      
      // 让 predecessor 的右指针指向 root，继续遍历左子树
      if (!predecessor.right) {
        predecessor.right = root;
        root = root.left;
      } else {
        // 说明左子树已经访问完了，我们需要断开链接
        result.push(root.val);
        predecessor.right = null;
        root = root.right;
      }
    
    } else {
      // 如果没有左孩子，则直接访问右孩子
      result.push(root.val);
      root = root.right;
    }
  }
  
  return result;
}

在这里插入图片描述

# 101. 对称二叉树

https://leetcode-cn.com/problems/symmetric-tree/ (opens new window)

# 【解法】递归

var isSymmetric = function(root) {
    function check(p, q){
        if(!p && !q) return true;
        if(!p || !q) return false;
        return p.val === q.val && check(p.left, q.right) && check(p.right, q.left);
    }
    return check(root, root);
};

在这里插入图片描述

# 【解法二】非递归

用一个队列

var isSymmetric = function(root) {

    return check(root.left, root.right)
};

function check(p,q){
    let queue = []
    queue.push(p)
    queue.push(q)
    while(queue.length > 0){
        p = queue.shift()
        q = queue.shift()
        if(!p && !q) continue
        if((!p || !q) || (p.val !== q.val)) return false
        queue.push(p.left)
        queue.push(q.right)

        queue.push(p.right)
        queue.push(q.left)
    }
    return true
}

在这里插入图片描述

# 102. 二叉树的层序遍历

https://leetcode-cn.com/problems/binary-tree-level-order-traversal/ (opens new window)

给你一个二叉树，请你返回其按层序遍历得到的节点值。（即逐层地，从左到右访问所有节点）。

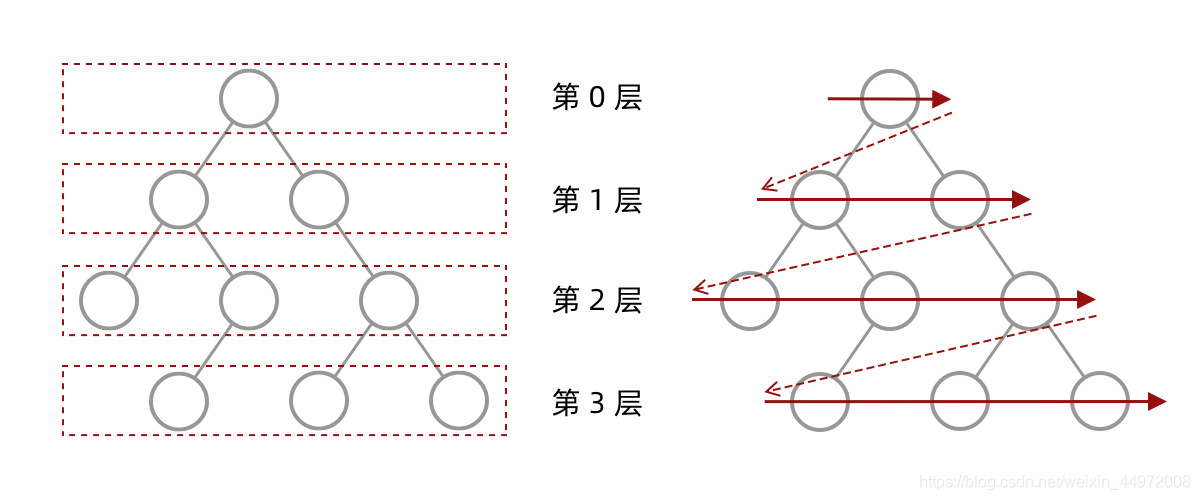
在这里插入图片描述

对比BFS的过程在这里插入图片描述需要改进前面说的 BFS

function BFS(root) {
  const queue = [];
  queue.unshift(root);
  
  while (queue.length > 0) {
    let len = queue.length;
    for (let i = 0; i < len; i++) {
      root = queue.pop();
      if (root.left) queue.unshift(root.left);
      if (root.right) queue.unshift(root.right);
    }
  }
}

在这里插入图片描述

# 【解法】广度优先搜索

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */

function levelOrder(root) {
  if(!root) return [];
  const result = [];
  const queue = [];
  queue.unshift(root);

  while (queue.length > 0) {
    let len = queue.length;
    let level = [];
    for (let i = 0; i < len; i++) {
      root = queue.pop();
      level.push(root.val);
      if (root.left) queue.unshift(root.left);
      if (root.right) queue.unshift(root.right);
    }
    result.push(level);
  }
  return result;
}

在这里插入图片描述

# 104. 二叉树的最大深度

递归方式有两种一种是【自顶向下】，一种是【自底向上】

先来看看自顶向下的递归方式

# 【解法一】递归【自顶向下】

“自顶向下” 意味着在每个递归层级，我们将首先访问节点来计算一些值，并在递归调用函数时将这些值传递到子节点。

所以 “自顶向下” 的解决方案可以被认为是一种前序遍历。

通用代码片段是这样的

1. return specific value for null node
2. update the answer if needed                      // answer <-- params
3. left_ans = top_down(root.left, left_params)		// left_params <-- root.val, params
4. right_ans = top_down(root.right, right_params)	// right_params <-- root.val, params
5. return the answer if needed                      // answer <-- left_ans, right_ans

本题代码

var maxDepth = function(root) {
    let result = 0
    function max_depth(root, depth){
    	// 递归出口，节点为空
        if(!root) return;
        // 【叶子节点】没有左孩子且没有右孩子
        if(!root.left && !root.right){
        	// 取最大深度
            result = Math.max(result, depth);
        }
        // 每递归一次深度+1
        max_depth(root.left, depth + 1);
        max_depth(root.right, depth + 1);
    }
    // 从根节点开始递归，深度为 1 
    max_depth(root, 1);
    return result;
};

在这里插入图片描述

# 【解法二】递归【自底向上】

“自底向上” 是另一种递归方法。在每个递归层次上，我们首先对所有子节点递归地调用函数，然后根据返回值和根节点本身的值得到答案。这个过程可以看作是后序遍历的一种。

通用代码片段

1. return specific value for null node
2. left_ans = bottom_up(root.left)			// call function recursively for left child
3. right_ans = bottom_up(root.right)		// call function recursively for right child
4. return answers                           // answer <-- left_ans, right_ans, root.val

本题代码

var maxDepth = function(root) {
    if(!root) return 0;
    let lMax = maxDepth(root.left);
    let rMax = maxDepth(root.right);
    return Math.max(lMax, rMax) + 1;
};

在这里插入图片描述

# 【解法三】迭代

# 112. 路径总和

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum ，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和 targetSum 。

# 【解法一】递归

var hasPathSum = function(root, targetSum) {
    // 节点不存在 返回false
    if(!root) return false
    // 左右子树都不存在，说明是叶子节点，判断是否符合条件
    if(!root.left && !root.right) return targetSum === root.val
	// 到这里就是：节点存在，左右子树存在一个或者都存在，也就是内部节点
    // 遍历左右子树，更新总和为 总和删除当前节点的值
    return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val)
};

在这里插入图片描述

# 【解法二】BFS - 队列

var hasPathSum = function(root, targetSum) {
    if(!root) return false
    // 创建两个队列
    // 用来存储节点
    let nodeQue = []
    // 用来存储根节点到这个节点的总和
    let valQue = []

    // 先将根节点入队列
    nodeQue.unshift(root)
    valQue.unshift(root.val)

    while(nodeQue.length > 0){
        // 将队头元素取出来得到节点root和值temp
        let root = nodeQue.pop()
        let temp = valQue.pop()

        // 如果这个节点是叶子节点（没有左右孩子）
        if(!root.left && !root.right){
            // 如何符合要求返回true 并 退出函数
            if(temp === targetSum) return true
            // 不满足要求 下面的都不会满足，就进行下一轮循环了
        }
        // 有左孩子就进来
        if(root.left){
            // 左孩子进队列
            nodeQue.unshift(root.left)
            // 保存此时路径总和
            valQue.unshift(root.left.val + temp)
        }
        // 有右孩子就进来
        if(root.right){
            // 右孩子进队列
            nodeQue.unshift(root.right)
            // 保存此时路径总和
            valQue.unshift(root.right.val + temp)
        }
    }
    // 循环走完都没有返回true就说明没有符合要求的路径总和
    return false

};

在这里插入图片描述

# 129. 求根到叶子节点数字之和

这题和112题的解法二一模一样

# 【解法一】BFS - 双队列

var sumNumbers = function(root) {
    let nodeQue = []
    let valQue = []
    let result = 0
    nodeQue.unshift(root)
    valQue.unshift(root.val)
    while(nodeQue.length > 0){
        let root = nodeQue.pop()
        let temp = valQue.pop()
        if(!root.left && !root.right) {
            result += temp
        }
        if(root.left){
            nodeQue.unshift(root.left)
            valQue.unshift(root.left.val + temp * 10)
        }
        if(root.right){
            nodeQue.unshift(root.right)
            valQue.unshift(root.right.val + temp * 10)
        }
    }
    return result
};

在这里插入图片描述

# 【解法二】递归

var sumNumbers = function(root) {   
    return dfs(root, 0)
};

function dfs(root, prevSum){
    // 节点不存在直接返回0
    if(!root) return 0
    // 根节点到当前节点数字之和
    let sum = prevSum * 10 + root.val

    // 如果是叶子节点，就返回sum
    if(!root.left && !root.right) return sum
    // 不是叶子节点，就递归，并把当前的和传给孩子节点
    return dfs(root.left, sum) + dfs(root.right, sum)
}

# 226. 翻转二叉树

# 【解法一】DFS 递归

var invertTree = function(root) {
    if(!root) return null

    const temp = root.left
    root.left = root.right
    root.right = temp
    
    invertTree(root.left)
    invertTree(root.right)

    return root
};

在这里插入图片描述

# 【解法二】BFS 队列

var invertTree = function(root) {
    if(!root) return null
    let queue = []
    const result = root
    queue.unshift(root)
    while(queue.length > 0){
        root = queue.pop()
        const temp = root.right
        root.right = root.left
        root.left = temp
        if(root.left) queue.unshift(root.left)
        if(root.right) queue.unshift(root.right)
    }
    return result
};

在这里插入图片描述

# 46. 全排列

# 【解法】回溯

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permute = function(nums) {
    // 保存结果数组，保存每个路径（排列）
    const result = []
    // 调用回溯函数，传入参数
    backtracking(nums, nums.length, [], [])
    // 返回结果数组
    return result


    // 定义回溯递归函数，传入数组，长度，节点是否被使用过的数组
    // used 用来标记节点是否被用过 path 用来存储路径，定义为一个栈
    function backtracking(nums, len, used, path){
    	// 递归出口
        // 如果到达叶子节点，将路径推入结果数组，并返回
        if(path.length === len) {
            result.push([...path])
            return
        }
        // 遍历候选字符
        for(let i = 0; i < len; i++){
            // 使用过就下一轮循环
            if(!used[i]){
            	// undefind和fasle都会进来
				// 这里说明这个数还没有被使用，入栈path
				path.push(nums[i])
				// 标记这个数被使用过了
				used[i] = true
				// 开始进行递归
				backtracking(nums, len, used, path)
				// 回溯【状态重置】撤销之前的操作
				path.pop()
				used[i] = false
			}
        }
    }
};

在这里插入图片描述

# 集合中的所有子集

var subsets = function(nums) {
    // 时间复杂度 O(2^n);
    let result = [[]];
    help(nums,0,[],result);
    return result;

    // 回溯法: 每遍历一个元素，我们可以决定它的添加与否
    function help(nums,idx,cur,result) {
        // 中止条件：当idx超出时，不在继续添加元素
        if(idx==nums.length) return;

        // 1.不添加这个元素
        help(nums,idx+1,cur,result);
        // 2. 添加这个元素
        cur = [...cur,nums[idx]];
        result.push(cur);
        help(nums,idx+1,cur,result);
    }
};

# 617. 合并二叉树

给定两个二叉树，想象当你将它们中的一个覆盖到另一个上时，两个二叉树的一些节点便会重叠。

你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠，那么将他们的值相加作为节点合并后的新值，否则不为 NULL 的节点将直接作为新二叉树的节点。在这里插入图片描述

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/merge-two-binary-trees

# 【解法】递归

/**
 * @param {TreeNode} root1
 * @param {TreeNode} root2
 * @return {TreeNode}
 */
var mergeTrees = function(root1, root2) {

    if(!root1) return root2;
    if(!root2) return root1;

    root1.val = root1.val + root2.val;

    root1.left = mergeTrees(root1.left, root2.left);
    root1.right = mergeTrees(root1.right, root2.right);

    return root1;
};

在这里插入图片描述

# 图类

链表概述

YK菌

# 树类

# 树的结构

# 树的遍历

# 深度优先遍历DFS （递归）

# 深度优先遍历DFS （栈）

# 广度优先遍历BFS （队列）

# 94. 二叉树的中序遍历

# 144. 二叉树的前序遍历

# 145. 二叉树的后序遍历

# 【解法一】递归DFS

# 【解法二】非递归 迭代法 - 栈

# 中序遍历

# 前序遍历

# 后序遍历（重难点）

# 【解法三】Morris 中序遍历

# 101. 对称二叉树

# 【解法】递归

# 【解法二】非递归

# 102. 二叉树的层序遍历

# 【解法】广度优先搜索

# 104. 二叉树的最大深度

# 【解法一】递归【自顶向下】

# 【解法二】递归【自底向上】

# 【解法三】迭代

# 112. 路径总和

# 【解法一】递归

# 【解法二】BFS - 队列

# 129. 求根到叶子节点数字之和

# 【解法一】BFS - 双队列

# 【解法二】递归

# 226. 翻转二叉树

# 【解法一】DFS 递归

# 【解法二】BFS 队列

# 46. 全排列

# 【解法】回溯

# 集合中的所有子集

# 617. 合并二叉树

# 【解法】递归

# 图类

# 【解法二】非递归迭代法 - 栈